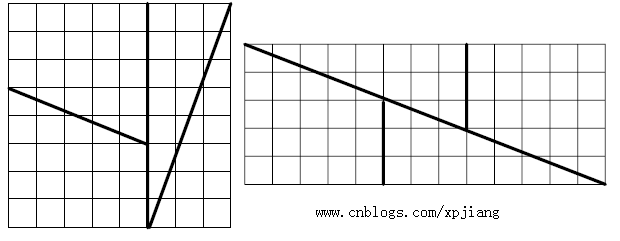
考虑下面的谬论，它是基于卡西尼恒等式的（对于斐波那契数列，当n ≥ 1 时，F(n+1)F(n-1) - [F(n)]^2 = (-1)^n。应用数学归纳法，我们很容易证明这个结论）。有一个8 × 8 的棋盘（更一般来说，任何划分为[F(n)]^2 个格子的F(n) 乘 F(n) 的棋盘）。按照下图的左半部分所示，将它切成两个梯形和两个三角形。然后再按照下图的右半部分把它们拼合起来。左边方块的面积是8 × 8 = 64， 而右边方块的面积是13 × 5 = 65。请解释该谬论。

 

 

 

 

 

 

 

 

 

 请选中下面的部分查看答案：

hints:这个谬论基于一个视觉陷阱，这四部分其实构不成一个矩形，因为三角形的直角边和梯形的腰不在一条直线上，因为如果它们在一条直线上的话，那么根据三角形相似，我们有3:8 = 5:13，注意到这是不可能的，因为39 ≠ 40。

(End_XPJIANG)